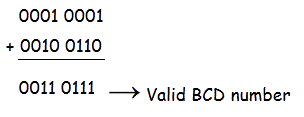BCD或二进制编码十进制| BCD转换加减

BCD或二进制编码的十进制是用二进制数或数字来表示十进制数的数字系统或代码。
一个十进制数包含10个数字(0-9)。现在可以从这10个十进制数中找到等价的二进制数。在的情况下BCD由四个二进制数字构成的二进制数，将是给定的十进制数字的等效码。在BCD我们只能使用0-1001的二进制数，它们分别是0-9的十进制等效数。假设一个数只有一个小数，那么它是等价的二进制编码的十进制是那个十进制数的四个二进制数字如果这个数包含两个十进制数字那么它是等价的BCD将是给定的十进制数的各自八二进制数。小数点的第一个数字是4，第二个数字是4。可以从示例中清除它。

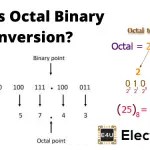
让(12)₁₀是其等价的十进制数二进制编码的十进制将00010010。来自L.S.B的4位二进制等价于2，接下来的4位二进制等价于1。
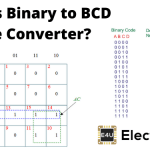
下表显示了二进制和BCD十进制数0到15的编码。
从下表，我们可以得出结论，9之后的十进制等效二进制数是4位的，而BCD是8位的。这是二进制数和二进制编码的十进制之间的主要区别。对于0到9位的十进制数，二进制数和BCD都是相等的，但是当十进制数大于1位时，BCD与二进制数不同。

十进制数	二进制数	二进制编码的十进制(BCD)
0	0000	0000
1	0001	0001
2	0010	0010
3.	0011	0011
4	0100	0100
5	0101	0101
6	0110	0110
7	0111	0111
8	1000	1000
9	1001	1001
10	1010	0001 0000
11	1011	0001 0001
12	1100	0001 0010
13	1101	0001 0011
14	1110	0001 0100
15	1111	0001 0101

BCD之外

与其他数字系统一样，在BCD中可能需要算术运算。BCD是一种有若干加法规则的数字代码。下面给出的规则分三个步骤，并举例说明BCD之外明确的。

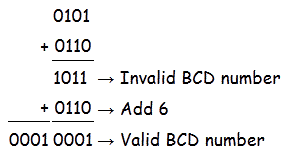
1. 首先，用二进制规则将给定的数相加。例如,
   
2. 第二步我们要判断加法的结果。这里有两个例子来描述规则BCD之外．在情况1中，两个二进制数相加的结果大于9，这对BCD数无效。但是情况2的加法结果小于9，这对BCD数有效。
3. 如果4位的加法结果大于9如果结果中有一个进位那么它是无效的我们必须加上6它的二进制等效值是(0110)₂对加法的结果。那么我们得到的结果将是一个有效的二进制编码数。在案例1中，结果是(1111)₂，它大于9，所以我们要加6或者(0110)₂到它。

如您所见，结果在BCD中是有效的。
但是在情况2中，结果已经是有效的BCD，所以不需要添加6。这就是BCD加法可以做到的。
现在可能会有一个问题，为什么要把6加到BCD加法中，而不是其他任何数。这样做是为了跳过二进制编码的十进制的6个无效状态，即从10到15，并再次返回到BCD码。
现在，可以从另外两个示例中清除BCD加法的思想。
例如:1
让0101和0110相加。

检查你的自我。

例如:2
现在把0001 0011加到00100110。


所以不需要加上6，因为两者都是小于(9)₁₀．这是BCD添加的过程。

BCD减法

有几种方法BCD减法．BCD减法可以通过1的补法和9的补法或10的补法来实现。在所有这些方法中，9种恭维法或10种恭维法是最简单的。我们将明确我们对这两种方法的想法BCD减法．

BCD减法

第一种方法BCD减法通过1的赞美方法。下面显示了该方法的几个步骤。他们是:-

1. 首先完成1的减法补充。
2. 然后将被减数加到另一个要做减法的数上。这叫做加法器1。
3. 在BCD减法中有一个术语EAC(end-around-进位)如果有进位，即如果EAC = 1，减法的结果是+ve，如果EAC = 0，结果是-ve。下表给出了EAC的规则。

   单个群体的携带	EAC = 1	EAC = 0
   1	将加法器1的实数转移到加法器2，将0000加进去	把加法器1的补加结果转移到加法器2，然后把1010加进去
   0	将加法器1的实数转移到加法器2中，加1010	把加法器1的补加结果转移到加法器2，然后把0000加到加法器2

4. 在最终的结果中，如果有任何进位出现，它将被忽略。

下面给出的例子可以清楚地说明BCD减法的思想。

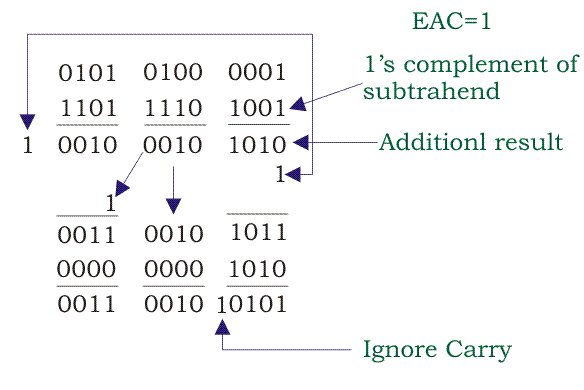
例子:- 1
在本例中，0101 0100 0001减去00100001 0110。

• 首先做减法1的补加，即1101 1110 1001，然后加到0101 0100 0001。这一步称为加法器1。
• 现在，在加法之后，如果任何进位发生，那么它将被添加到MSB的下一组数字中。然后检查EAC。这里EAC = 1。所以加法的结果是正的，加法器1的真结果将被转移到加法器2。
• 现在来自LSB的通知。有三组四位数字。1010和1011是第一组数字，因为它没有进位。加法的结果就是最终的答案。
• 进位1将被忽略，因为它来自规则。
• 现在来看下一组数字。将0000添加到0010，得到结果0010。这又是最后的结果。
• 现在再次移动到下一组这里0000也被添加到0011得到最终结果0011。
• 您可能已经注意到，这两组加了0000，因为第一个加法器的结果不包含任何进位。因此加法器2的结果就是BCD减法的最终结果。

因此,
现在你可以检查自己了。

我们知道541−216 = 325，因此我们可以说BCD减法是正确的。

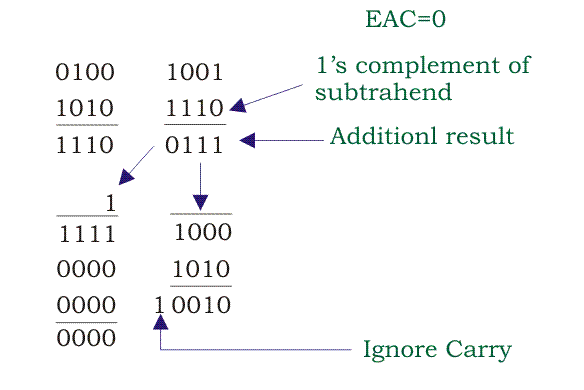
例子:- 2
在本例中，让0100 1001减去0101 0001。

• 根据规则，首先完成1的减法补算。然后完成添加并检查结果。这里EAC = 0，所以总的结果是-ve。
• 现在看看LSB的加法器1的结果。1的补值0111被转移到加法器2，并与1010相加，因为按照规则它没有加进位。答案就是最终的结果。
• 现在移动到加法器1的下一个结果，即1110。这里加了1，这是前一个结果的进位。然后它的值是1的增值，即0000，它被加到0000。加法器2的结果是最终结果。这是BCD减法的最终结果。
  
• 现在你可以再次检查自己。等号的十进制减法是49和51。因此49 -51 = -2。所以我们的结果是正确的。
  

BCD减法:2

在2^nd我们将在9的补法中做BCD减法。

• 这里的方法很简单。首先找出给定的二进制编码的十进制(BCD)码的十进制等价。
• 然后减去9的补数完成，然后把这个结果加到要做减法的数上。
• 如果有任何进位，则可以将进位加到减法的结果中。

这个想法可以从下面的例子中得到澄清。
设(0101 0001)−(0010 0001)为给定减法。

• 我们可以看到51和21是给定BCD码的十进制值。然后减去9，即99−21 = 78。
• 这一附加价值是与51。也就是51 + 78 = 129。
• 在这个结果中，MSB即1是进位。这个进位将加到29。因此29 + 1 = 30，这就是BCD减法．
• 小数结果将被转换为BCD代码以获得BCD中的结果。因此，从这个例子我们可以得出BCD减法的最终结果即

二进制编码的十进制减法使用10的补加法和使用9的补加法是一样的，唯一的区别是我们不用9的补加法，而是用10的减法的补加法。

BCD Comversion

BCD转换是非常简单的。在BCD转换的情况下，首先将十进制等价于BCD代码被发现，然后，该十进制数字可以改变为任何其他数字系统的需要。要了解数字系统的转换方法，你可以阅读这个主题二进制数字系统．