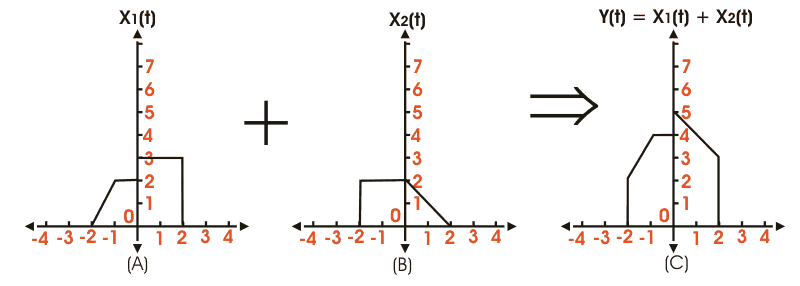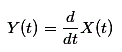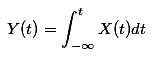一种信号,包括作为任意数量的独立变量的函数表示的一组信息,其可以作为系统的输入,或者从系统的输出导出,实现其真正的实用工具。我们从复杂系统中获得的信号可能并不总是处于我们想要的形式,
∴很好地熟悉一些基本信号操作可能真的可以帮助提高信号的可理解性和适用性。
从一个信号到另一个信号的数学变换可以表示为
其中,y(t)表示从原始信号x(t)导出的修改信号,只具有一个独立变量t。
这基本信号操作可以广泛归类如下。
对从属变量执行的基本信号操作
在该转换中,仅修改正交轴值,即信号的幅度发生变化,对水平轴值或信号的周期性没有影响。
- 信号的幅度缩放。
- 添加信号。
- 信号乘法。
- 信号的分化。
- 信号集成。
让我们详细介绍这些类型。
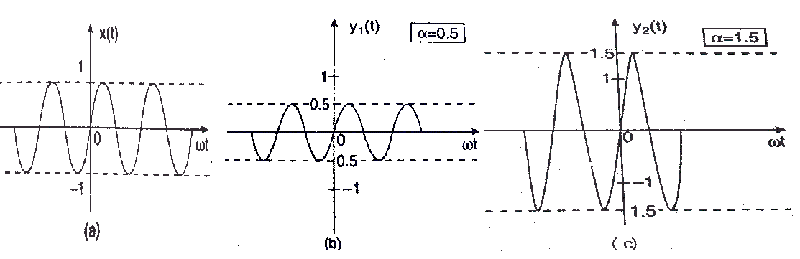
信号的幅度缩放
幅度缩放是对信号执行以改变其强度的非常基本的操作。它可以在数学上表示为y(t)=α.x(t)。
这里,α.是缩放因子,其中: -
α<1→信号衰减。
α> 1→信号被放大。
这在图中示出了,其中当α= 0.5在图(B)中的α= 0.5时,信号被衰减,并且当如图(c)中的α= 1.5时放大。
添加信号
该特定操作涉及在每个时间的时间或在信号之间常见的任何其他独立变量的两个或更多个信号的增加的幅度。在下图中说明信号的添加,其中x1(t)和x2(t)是两次依赖的信号,对它们进行额外的操作我们得到,
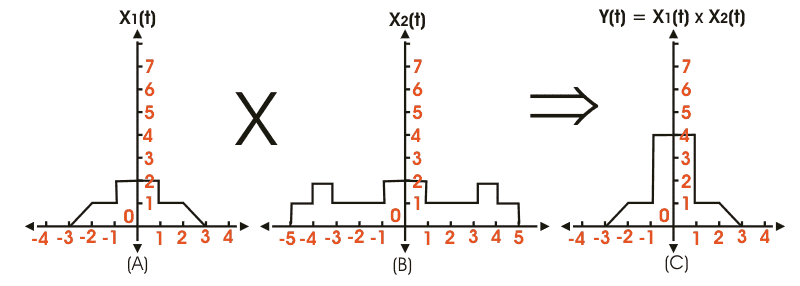
信号乘法
类似于信号的乘法也属于基本信号操作的类别。这里,在每个时间或任何其他独立变量的情况下乘以两个或更多个信号的幅度,在信号之间是常见的。得到的信号我们获得的值等于每个时间实例的父信号幅度的乘积。信号的乘法在下图中示出,其中x1(t)和x2(t)是两个时间依赖的信号,在执行乘法操作之后,我们得到的,
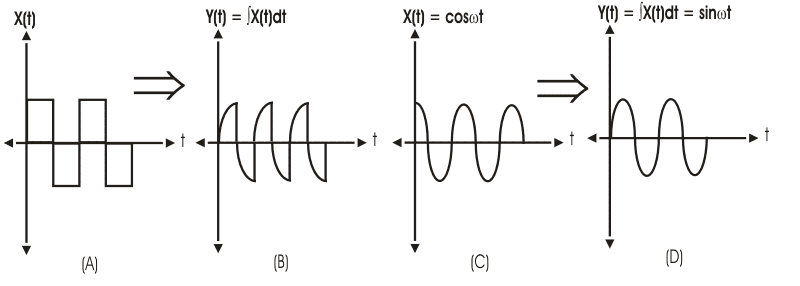
信号的分化
对于信号的分化,必须注意,该操作仅适用于连续信号,因为不能区分离散函数。我们对差异进行差异的修改信号在所有时间实例中都具有父信号的切向值。在数学上,它可以表示为: -
标准方形和正弦波的分化如下图所示。
信号集成
与差异化一样,信号的集成也适用于连续时间信号。集成的极限将来自 - ∞到现时间t的实例。它在数学上表示,
一些连续时间信号的集成如下图所示。
对从属变量执行的基本信号操作
这与上述情况完全相同,这里通过修改水平轴值来改变信号的周期性,而幅度或强度保持恒定。这些都是:-
- 信号的时间缩放
- 信号的反射
- 信号的时间换档。
让我们详细介绍这些操作。
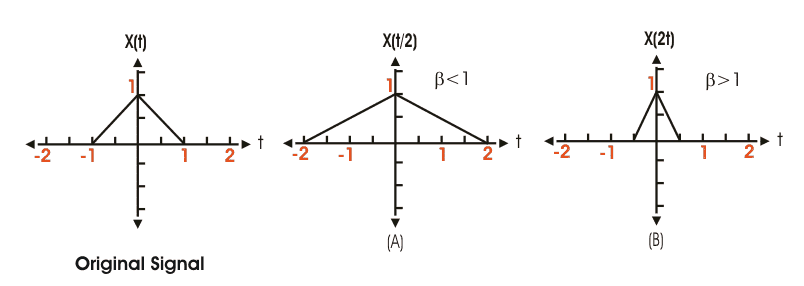
信号的时间缩放
信号信号的时间缩放涉及修改信号的周期性,保持其幅度常数。它的数学上表达为,
其中,x(t)是原始信号,β是缩放因子。
如果β> 1意味着,则信号被压缩,β1意味着,信号被扩展。这是图解的,以便更好地理解。
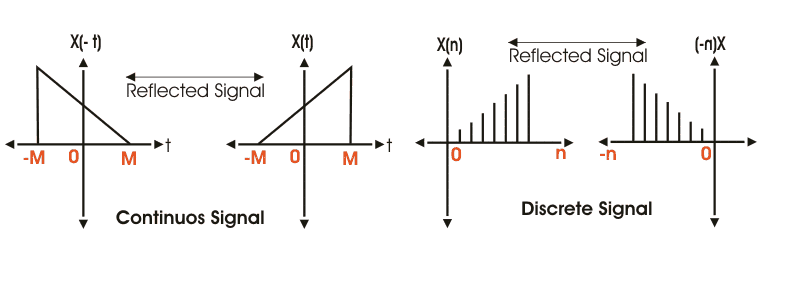
信号的反射
信号的反射是适用于连续和离散信号的非常有趣的操作。这里在这种情况下,垂直轴用作镜子,并且获得的变换图像是父信号的镜像。
它可以定义为y(t)= x( - t)其中,x(t)是原始信号。
但是,如果反射信号x( - t)= x(t);然后它被称为偶数信号。
其中x( - t)= - x(t);然后其称为奇数信号。
它绘图地解释为,
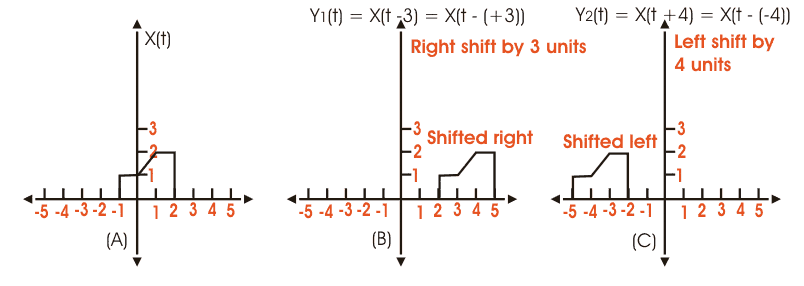
时间转移信号
信号的时间变化可能是最重要的,而且最广泛使用基本信号操作。它通常用于快速前进或延迟信号,就像在大多数实际情况下都是必要的。时间转移在数学上表达为,
其中,x(t)是原始信号,而t0.代表时间转变。
对于信号x(t),如果位置移位0.> 0.然后将信号置于右移或延迟。
以同样的方式,如果是0.<0,意味着信号左移或延迟。这已经示意性地在下图中解释。当原始信号(a)的情况下,右移,也分别在图(b)和(c)中移位。