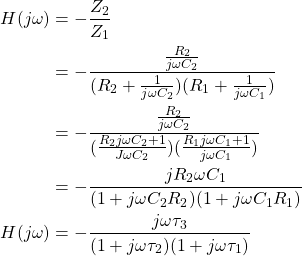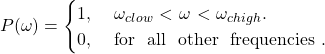带通滤波器:它是什么?(电路、设计和传递功能betway网页版 - betway网页版,betway必威体育精装版,必威亚洲体育

内容

什么是带通滤波器?

带通滤波器(也称为BPF或通带滤波器)定义为允许特定频率范围内的频率，并拒绝(衰减)该范围外的频率的设备。

的低通滤波器用于隔离频率高于截止频率的信号。类似地,高通滤波器用于隔离频率低于截止频率的信号。

高通滤波器和低通滤波器通过串级连接形成另一个滤波器，使特定频率范围或频带的信号衰减，使该频带以外的信号衰减。这种类型的过滤器被称为带通滤波器。

带通滤波器有两个截止频率。第一个截止频率来自一个高通滤波器。这将决定一个频带的更高频率极限，即所谓的更高截止频率(fc-high)。第二个截止频率来自低通滤波器。这将决定频带的下限频率，即已知的下限截止频率(fc-low)。

带通滤波电路

带通滤波器是低通滤波器和高通滤波器的组合。因此，电路图包含了高通和低通滤波器的电路。无源RC带通滤波器的电路图如下图所示。

电路图的前半部分是一个无源RC高通滤波器。该滤波器将允许频率高于较低截止频率(fc-low)的信号。衰减频率低于(fc-low)的信号。

$F_c_l_o_w = \frac{1}{2 \pi R_1 C_1}$

电路图的第二部分是一个无源RC低通滤波器。该滤波器将允许频率低于较高截止频率(fc-high)的信号。它将衰减频率高于(fc-high)的信号。

$F_c_h_i_g_h = \frac{1}{2 \pi R_2 C_2}$

带通滤波器允许信号通过的频带或频率区域，称为带宽。带宽是截止频率的高低之差。

$带宽= F_c_h_i_g_h - F_c_l_o_w$

带通滤波器类型

带通滤波器的设计电路有很多种。让我们详细解释滤波器电路的主要类型。

有源带通滤波器

有源带通滤波器是由高通和低通滤波器与放大元件级联而成，如下图所示。

有源带通滤波器的电路图分为三部分。第一部分是一个高通滤波器。然后运放用于放大。电路的最后一部分是低通滤波器。下图是有源带通滤波器的电路图。

无源带通滤波器

无源滤波器只使用无源组件，如电阻，电容器,电感器．因此，无源带通滤波器也使用无源元件，它不使用运放进行放大。因此，就像有源带通滤波器一样，无源带通滤波器中不存在放大部分。

无源带通滤波器是由无源高通滤波器和无源低通滤波器组成。因此，电路图中还包含了高通和低通滤波器的电路。

电路的前半部分用于无源高通滤波器。第二部分是无源低通滤波器。

RLC带通滤波器

顾名思义，这个带通滤波器只包含电阻、电感和电容。这也是一个无源带通滤波器。

根据RLC的连接情况，RLC带通滤波器有两种电路配置。在第一配置中，串联LC电路与负载电阻串联连接。所述第二组态为并联LC电路，所述LC电路与负载电阻并联连接。

串并联RLC带通滤波器的带宽如下式所示。

串联RLC滤波器的带宽

$\Delta \omega = \frac{R_L}{L}$

两种构型的角频方程是相同的，方程为

并行RLC滤波器的带宽

$\Delta \omega = \frac{1}{R_L C}$

宽带通滤波器

根据带宽大小可分为宽带滤波器和窄带滤波器。如果q因子小于10，该滤波器称为宽通滤波器。顾名思义，宽带通滤波器的带宽是宽的。

在这种类型的滤波器中，高通和低通滤波器是不同的部分，就像我们在无源带通滤波器中看到的那样。在这里，两个过滤器都是无源的。

另一种电路安排可以通过使用有源高通和有源低通滤波器来实现。该滤波器的电路图如下图所示，其前半部分为有源高通滤波器，下半部分为有源低通滤波器。

由于滤波器各部分的不同，使得电路易于设计出宽带宽范围。

窄带通滤波器

质量因数大于10的带通滤波器。这个滤波器的带宽很窄。因此，它允许信号的频率范围很小。它有多个反馈。这个带通滤波器只使用一个运放。

这种带通滤波器也被称为多重反馈滤波器，因为有两条反馈路径。

在此带通滤波器中，运放采用非反相模式。带通滤波器电路图如下图所示。

下图区分宽通滤波器和窄通滤波器的频率响应。

带通滤波器传递函数

一阶带通滤波器传递函数

一阶带通滤波器是不可能的，因为它至少有两个节能元件(电容或电感)。因此，二阶带通滤波器的传递函数推导如下:

二阶带通滤波器传递函数

二阶带通滤波器传递函数如下所示和推导。

$Z_1 = R_1 + \压裂{1}{j \omega C_1}$

$Z_2 = R_2 || \frac {1}{j \omega C_2}$

$\ [Z_2 = \压裂{R_2 \压裂{1}{j \ω₂}}{R_2 + \压裂{1}{j \ω₂}}\]$

（1) ${方程*}\ \开始开始{对齐}H (j \ω)& = - \压裂{Z_2} {Z_1 } \\ &= - \ 压裂{\压裂{R_2} {j \ω₂}}{(R_2 + \压裂{1}{j \ω₂})(R_1 + \压裂{1}{j \ωc₁ })} \\ &= -\ 压裂{\压裂{R_2} {j \ω₂}}{(\压裂{R_2 j \ω₂+ 1}{j \ω₂})(\压裂{R_1 j \ωc₁+ 1}{j \ c₁ω })} \\ &= - \ 压裂{j R_2 \ωc₁}{(1 + j \ω₂R_2) (1 + j \ωc₁R_1)} \ \ H (j \ω)& = - \压裂{j \ω\ tau_3} {(1 + j \ω\ tau_2) (1 + j \ω\ tau_1)} \{对齐}\{方程*}结束结束$

在那里,

$\ [\ tau_1 = R_1 c₁\四\ tau_2 = R_2 c₂\四\ tau_3 = R_3 C_3 \]$

$\ [\ omega_1 = \压裂{1}{\ tau_1} \四\ omega_2 = \压裂{1}{\ tau_2} \四\ omega_3 = \压裂{1}{\ tau_3} \]$

对于带通滤波器，必须满足以下条件:

$\omega_1， \ omega__2 > \omega_3$

带通滤波器截止频率

带通滤波器是由两个滤波器组成的。因此，它有两个截止频率。一个截止频率由高通滤波器导出，记为F_c-high．该滤波器允许频率大于F的信号_c-high．F的值_c-high由下式计算。

$F_c_l_o_w = \frac{1}{2 \pi R_1 C_1}$

第二个截止频率由低通滤波器导出，记为F_c-low．该滤波器允许频率低于F的信号_c-low．F的值_c-low由下式计算。

$F_c_h_i_g_h = \frac{1}{2 \pi R_2 C_2}$

滤波器在频率F之间工作_c-high和F_c-low．这些频率之间的范围称为带宽。因此，带宽定义为:

$带宽= F_c_h_i_g_h - F_c_l_o_w$

高通滤波器的截止频率决定了带宽的下限，低通滤波器的截止频率决定了带宽的上限。

带通滤波器波德图或频率响应

上图显示了波德图或者带通滤波器的频率响应和相位图。滤波器将允许信号的频率在带宽之间。

该滤波器对频率低于高通滤波器截止频率的信号进行衰减。直到信号到达FL，输出以+20 DB/Decade的速率增加，与高通滤波器相同。

在此之后，输出以最大增益连续，直到达到低通滤波器的截止频率或F点_H．然后输出将以- 20db /Decade的速率下降，与低通滤波器相同。

带通滤波器是一个二阶滤波器，因为它在电路图中有两个无功元件。因此，相位差是一阶滤波器的两倍，为180˚。

直到中心频率，输出信号与输入的距离为90˚。在中心频率处，输出信号与输入信号相位一致。因此，相位差为0˚。

在中心频率之后，输出信号滞后输入90˚。

理想带通滤波器

一个理想的带通滤波器允许信号精确地从F_l类似于阶跃响应。信号正好允许在F点_l斜率为0 DB/Decade。它会使频率大于F的信号突然衰减_H．

理想带通滤波器的频率响应如下图所示。这种类型的响应不能产生实际的带通滤波器。

带通滤波器方程

当信号频率在带宽范围内时，滤波器将允许信号具有输入阻抗。当信号频率在带宽之外时，输出为零。

用于带通滤波器;

（2) $开始\ P{方程*}(\ω)= \{病例}1开始,& \文本{$ \ omega_{克洛}< $ $ $ $ \ω< $ $ $ $ \ omega_ {chigh}}。0， & text{用于所有其他频率}。结束\{病例}\{方程*}结束$

带通滤波器的应用

带通滤波器的应用如下:

带通滤波器广泛应用于音频放大电路中。例如，使用扬声器只播放所需的频率范围，而忽略其余的频率。
它是用光学的激光、激光雷达等。
这些滤波器用于通信系统中选择具有特定带宽的信号。
它用于音频信号处理。
它还用于优化接收机的信噪比和灵敏度。

带通滤波器设计实例

现在你们熟悉带通滤波器了。让我们为特定带宽设计一个滤波器。我们将制作一个滤波器，允许频率在80hz到800hz范围内的信号。

F1 = 80 Hz
F2 = 800 Hz

对于这个例子，我们将为给定的频率范围做一个简单的无源RC滤波器。我们需要计算，R1 C1 R2 C2的值。

$f_1 = \frac{1}{2 \pi R_1 C_1}$

$R_1 C_1 = \frac{1}{2 \pi f_1}$

同样的,

$R_2 C_2 = \frac{1}{2 \pi f_2}$

我们必须假定电阻或电容的值。这里，我们假设C1和C2的值。为了简单计算，我们假设C1和C2的值是相同的，即10^－6F.根据C1, C2, F1, F2的值计算电阻值。

$c_1 = c_2 = 10^{-6} f$

因此,

$R_1 = \frac{1}{2 \pi f_1 C_1}$

$\ [R_1 = \压裂{1}{2 \π\乘以80 \ * 10 ^ {6}}\]$

$R_1 \约500 \Omega$

同样的,

$R_2 = \frac{1}{2 \pi f_2 C_2}$

$\ [R_2 = \压裂{1}{2 \π\乘以800 \ * 10 ^ {6}}\]$

$R_2 \约5000 \Omega$

现在，我们有了所有的值，通过这些值，我们可以做一个滤波器，它允许特定带宽的信号。