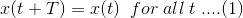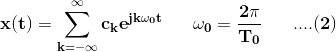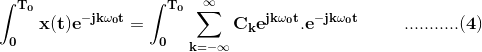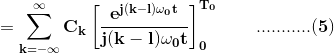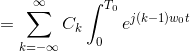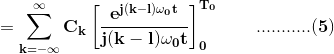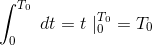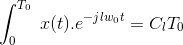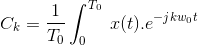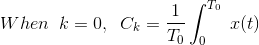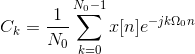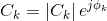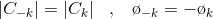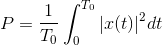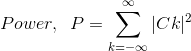分析指数傅里叶系列

傅里叶系列一目了然

如果存在正则非零值，则据说连续时间信号x（t）是周期性的

正如我们所知，任何周期性信号都可以分为谐波相关的正弦曲线或复杂的指数，只要它满足了dirichlet的条件。调用这种分解的表示傅里叶系列。
两种类型傅里叶系列代表在那里。两者都相当于彼此。

• 指数傅里叶系列
• 三角傅里叶系列

这两个表示结果都具有相同的结果。根据信号类型，我们根据方便起见。

指数傅里叶系列

以周期性信号分析指数傅里叶系列在以下三个阶段：

1. 定期信号的表示。
2. 周期信号的幅度和相位光谱。
3. 周期信号的功率内容。

定期信号的表示

傅立叶系列中的周期性信号可以在两个不同的时间域中表示：

1. 连续时间域名。
2. 离散时域。

连续时间域名

复杂指数傅里叶系列具有基本时段T的周期性信号x（t）的表示_O.是（谁）给的

其中，c被称为复杂的傅里叶系数并且由，

哪里∫_0.^T._0.，表示任何一个时期的整体，0到t_0.或者_0./ 2到t_0./ 2是常用于整合的限制。
可以导出等式（3）将等式（2）的两侧乘以e^{（-JLΩ._0.T）}并在一段时间内整合。

在互换求和和整合r.h.s.的情况下，我们得到了



当k≠l时，（5）的右侧在下限和上限时得到的右侧产生零。另一方面，如果k = l，我们有

因此等式（4）减少到



这表示在一段时间内的平均值x（t）。
当x（t）是真实的，

其中，*表示缀合物

离散时域

离散的离散表示非常类似于连续时域的周期信号的傅里叶表示。
周期性序列X [n]的离散傅立叶系列表示，基本时期n_O.是（谁）给的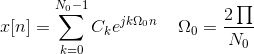
在哪里，C_K.，是傅里叶系数，并由

这可以以与我们在连续时域中导出的方式相同的方式导出。

周期信号的幅度和相位光谱

我们可以表达复杂的傅里叶系数c_K.作为

绘图| c_K.|与角频率w称为周期性信号x（t）的幅度谱，以及ф的图_K.，与w称为x（t）的相位谱。由于索引k仅采用整数，因此幅度和相位光谱不是连续曲线，而是仅在离散频率KΩ上出现_0.因此，它们被称为离散频谱或线谱。
对于真正的周期性信号x（t）我们有c_k= C._K.^*。因此，

因此，幅度频谱是均匀的ω，并且相位谱是奇数函数0.对于真正的周期性信号。

周期信号的功率内容

平均数周期信号的功率内容是（谁）给的

如果x（t）由复杂的指数傅里叶系列表示，那么

这种等式称为Parseval的身份或Parseval定理。